Premialab offers a comprehensive platform for systematic strategies, partnering with 18 leading index sponsors to provide consolidated data on over 5,000 Quantitative Investment Strategies (QIS). Using this extensive database, Premialab has developed a unique factor model capturing the consensus implementation across providers whilst eliminating disruptive noise and modelspecific interference using a rigorous three-step statistical analysis. The existing Premialab Pure Factors® framework includes Carry, Low Volatility, Momentum, Quality, Size, Value, and Volatility across five asset classes – Equity, Fixed Income, Credit, Commodity, and Foreign Exchange.
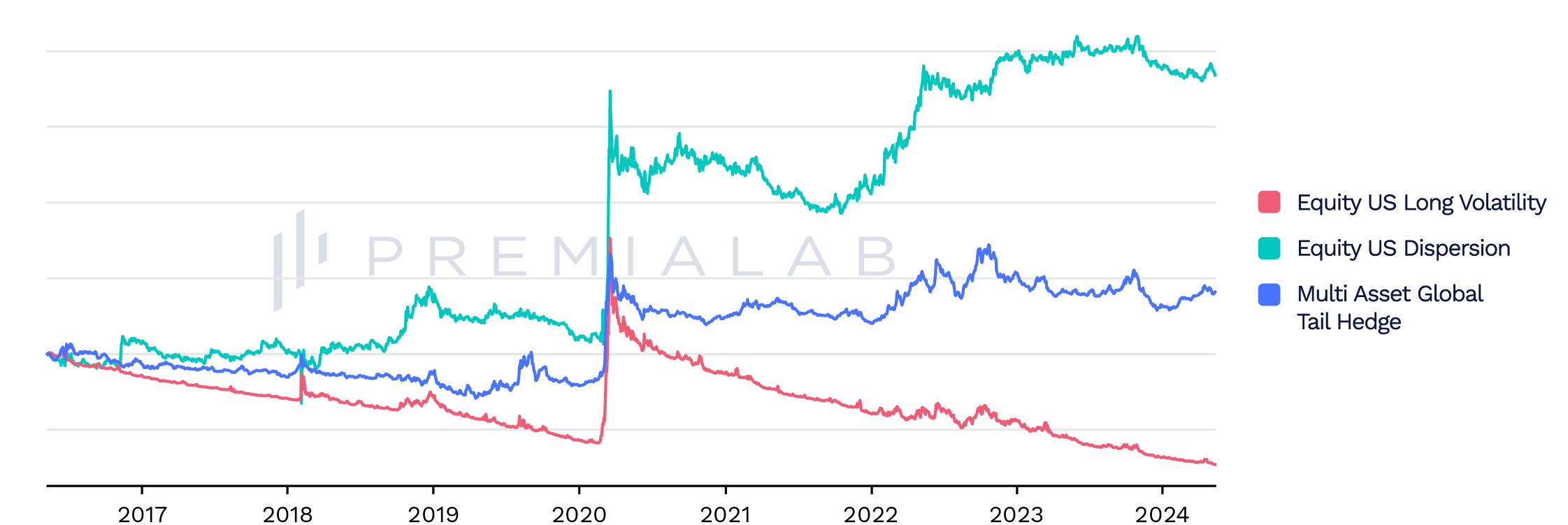
In the face of volatile market conditions and heightened economic uncertainty, institutional investors have increasingly turned to customized tail risk hedging strategies to buy positive convexity for safeguarding their portfolios. The recent spate of financial crises – including the 2022 UK mini-budget crisis, 2020 Covid-19 and 2018 Volmageddon – has demonstrated the limitations of relying solely on diversification to provide adequate protection during periods of severe market stress. Recognizing the growing market demands, banks have responded by broadening their systematic strategy offerings with defensive implementations. Premialab has expanded the Pure Factors® suite with three new additions to cover tail risk hedging implementations.
-
Premialab Equity US Long Volatility Pure Factor®
-
Premialab Equity US Dispersion Pure Factor®
-
Premialab Multi-Asset Global Tail Hedge Pure Factor®
The construction of Premialab Pure Factors® adheres to a three-step methodology described in the Premialab white paper on Advanced Factor Analytics (Trecourt, 2022): top-down strategy filtering, consensus extraction using Principal Component Analysis (PCA), and quarterly weight rebalancing. The three Premialab Downside Protection Pure Factors® follow a similar construction process. Long Volatility and Tail Hedge factors undergo an additional layer of processing, making them a composite of different implementations as further explained in this paper.